Abstract Data Structures

You will learn what an ADT is and the various types and uses cases for them.

What Are Abstract Data Structures?

Abstract data structures are like blueprints for organizing and managing data. They define how data is stored, accessed, and manipulated, without worrying about the nitty-gritty details of implementation.

Types of Abstract Data Structures

Stack

• What It Is: Think of a stack like a stack of pancakes. You add (push) pancakes on top and take (pop) them from the top. It's a Last In, First Out (LIFO) structure.
• Why It's Useful: Stacks are great for scenarios where you need to reverse things or keep track of operations, like undo features in software or backtracking algorithms.

<-- pop |__7__| <-- push
        |__6__|
        |__5__|
        |__4__|
        |__3__|
        |__2__|
        |__1__|

stack.py

class Stack:
    def __init__(self):
        self.items = []
    def push(self,item):
        self.items.append(item)
    def pop(self):
        if len(self.items) != 0:
            self.items.pop()
        else:
            print('Empty')
    def peek(self):
        if len(self.items) != 0:
            return self.items[:-1]
    def search(self):
        pass
    def empty(self):
        return len(self.items) == 0
    def size(self):
        return len(self.items)

s = Stack()

s.push(1)
s.push(2)
s.push(3)
s.push(4)

print(s.items)

s.pop()
print(s.items)
s.pop()
print(s.items)
s.pop()
print(s.items)
s.pop()
print(s.items)
s.pop()

stack2.py

class Stack:
    def __init__(self):
        self.items = []
        self.size = 0
    def push(self,item):
        self.items.append(item)
        self.size = len(self.items) + 1
    def pop(self):
        if not self.empty():
            self.items.pop()
            self.size = len(self.items) - 1
        else:
            print('Empty')
    def peek(self):
        if not self.empty():
            return self.items[:-1]
    def search(self):
        pass
    def empty(self):
        return self.size == 0
    def size(self):
        return len(self.items)

s = Stack()
s.items = [1,2,3]
s.push(4)
print(s.items)

s.pop()

print(s.items)

print(s.empty())

print(s.size)

browser_stack.py

class BrowserStack:
    def __init__(self):
        self.items = []
    def push(self,item):
        self.items.append(item)
    def pop(self):
        if len(self.items) != 0:
            self.items.pop()
        else:
            print('Empty')
    def peek(self):
        if len(self.items) != 0:
            return self.items[:-1]
    def search(self):
        pass
    def empty(self):
        return len(self.items) == 0
    def size(self):
        return len(self.items)

s = BrowserStack()

s.push('http://www.google.com')
s.push('https://tdwebdevcourse.netlify.app/')
s.push('https://vitepress.dev/')
s.push('https://vuejs.org/guide/introduction.html')

print(s.items)

s.pop()
print(s.items)
s.pop()
print(s.items)
s.pop()
print(s.items)
s.pop()
print(s.items)
s.pop()

Queue

• What It Is: Imagine a line at a coffee shop. The first person in line is served first, and new people join the end of the line. It's a First In, First Out (FIFO) structure.
• Why It's Useful: Queues are perfect for managing tasks in order, like print jobs or customer service requests.

<-- dequeue |__1__|__2__|__3__|__4__|__5__|__6__|__7__| <-- enqueue

queue.py

class Queue:
    def __init__(self):
        self.items = []
        self.size = 0
    def enqueue(self,item):
        self.items.append(item)
    def dequeue(self):
        self.items.pop(0)
    def front(self):
        return self.items[0]
    def rear(self):
        return self.items[-1]

q = Queue()

q.enqueue(1)
q.enqueue(3)
q.enqueue(4)
q.enqueue(5)
q.enqueue(6)
q.enqueue(7)
q.enqueue(8)

q.dequeue()
print(q.items)
q.dequeue()
print(q.items)
q.dequeue()
print(q.items)
q.dequeue()
print(q.items)
q.dequeue()
print(q.items)
q.dequeue()
print(q.items)
q.dequeue()
print(q.items)

music_queue.py

class MusicPlaylist:
    def __init__(self):
        self.items = []
        self.size = 0
    def enqueue(self,item):
        self.items.append(item)
    def dequeue(self):
        return None if len(self.items) == 0 else self.items.pop(0)
    def front(self):
        return self.items[0]
    def rear(self):
        return self.items[-1]

q = MusicPlaylist()

q.enqueue({'song_title': "Here we go again"})
q.enqueue({'song_title': "It takes three"})
q.enqueue({'song_title': "At the carnival"})
q.enqueue({'song_title': "This is where we part"})
q.enqueue({'song_title': "He'll do it again"})
print(q.items)
q.dequeue()
print(q.items)
q.dequeue()
print(q.items)

print({'front': q.front()},{'rear': q.rear()})

q.dequeue()
print(q.items)
q.dequeue()
print(q.items)
q.dequeue()
print(q.items)
q.dequeue()

List

• What It Is: A list is a collection of items that you can access by their position (index). Think of it like a shopping list where each item has a specific spot.
• Why It's Useful: Lists are versatile and easy to use for storing and accessing a sequence of elements.

Linked List

• What It Is: A linked list is like a treasure hunt. Each item (node) has a value and a pointer to the next item. It’s a sequence of nodes connected together.
• Why It's Useful: Linked lists are great for dynamic data where you need efficient insertions and deletions, like managing playlists or navigation in a browser’s history.

class Node:
    def __init__(self):
        self.data = None
        self.next = None

class LinkedList:
    def __init__(self):
        self.items = []
    def add(self,item):
        self.items.append(item)

node = Node()
node2 = Node()

linked_list = LinkedList()
linked_list.add(node,node2)

Note

Useful for getting the next item. Used for stacks and queues. Sorting and Search algorithms. Some examples of linked lists are Music playlist (next) and Course (next section)

Here is a more visual representation of how a linked list works, but the code above is the best way to implement a linked list.

regularList = ['joe','sam','rachel']

linkedlist = [
    ['joe',1],
    ['sam',2],
    ['sam',3],
    ['sam',4],
    ['sam',4],
    ['sam',6],
    ['rachel',None]
]

doublyLinkedlist = [
    ['joe',1,None],
    ['sam',2,0],
    ['sam',3,1],
    ['sam',4,2],
    ['sam',5,3],
    ['sam',6,4],
    ['rachel',None,5]
]

for item in doublyLinkedlist:
    if item[2] == None:
        print('This is the first node')
        print(item)
    elif item[1] == None:
        print('This is the last node')
        print(item)

Doubly Linked List

• What It Is: A doubly linked list is like a two-way street. Each node has pointers to both the next and previous nodes, allowing traversal in both directions.
• Why It's Useful: These are useful when you need to navigate back and forth, like in an undo/redo feature or a browser’s forward/backward navigation.

doubly.py

class Node:
    def __init__(self):
        self.data = None
        self.next = None
        self.prev = None

class DoublyLinkedList:
    def __init__(self):
        self.items = []
    def add(self,item):
        self.items.append(item)

node = Node()
node2 = Node()

linked_list = LinkedList()
linked_list.add(node,node2)

Graph

• What It Is: Think of a graph like a social network. It consists of nodes (vertices) connected by edges (links). Nodes represent entities, and edges represent relationships.
• Why It's Useful: Graphs are used in social networks, navigation systems (like GPS), and network topology, where relationships between entities are important.

graph.py

graph = { }

graph['you'] = ['alice','bog','claire']
graph['bob'] = ['sam','peggy']
graph['alice'] = ['peggy']
graph['claire'] = ['thomas','johnny']
graph['sam'] = []
graph['thomas'] = []
graph['peggy'] = []
graph['johnny'] = []

# print(graph)

for i in graph:
    print(i)
    print(graph[i])

Tree

• What It Is: A tree is like a family tree. It has a root node and branches out to child nodes, with each node having zero or more children. It's a hierarchical structure.
• Why It's Useful: Trees are great for hierarchical data like file systems, organizational structures, and decision-making processes.

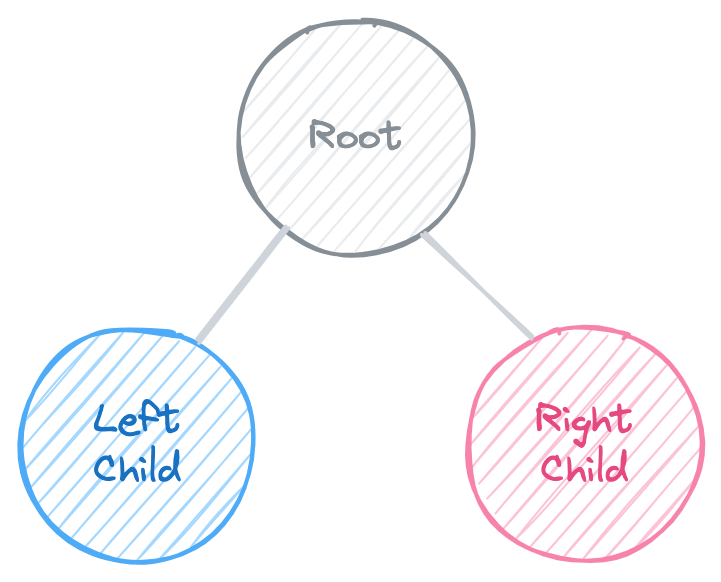
Graph VS Tree

Here's how trees and graphs differ in Python code:

Structure:

• Trees: Hierarchical. They have a single root node, and nodes can have zero or more children. The children cannot loop back to the parent or any other ancestor. Think of it like an organizational chart, where the CEO is at the root and employees branch out below them.
• Graphs: More flexible. They consist of nodes (vertices) connected by edges. These edges can be directed (one-way connection) or undirected (two-way connection). There can be cycles in graphs, where a node can be connected back to itself or an ancestor. Imagine a social network, where people (nodes) are connected by friendships (edges), and these connections can go in any direction.

Implementation:

• Trees: Typically implemented using a class with attributes for data and child nodes, or using nested dictionaries where keys represent node data and values hold child references.
• Graphs: Often implemented using libraries like NetworkX which provide specialized data structures and algorithms for graphs. You can also use dictionaries or adjacency lists to represent simpler graphs.

Use Cases:

• Trees: Used for representing hierarchical relationships, searching sorted data (e.g., binary search trees), and parsing expressions.
• Graphs: Used for modeling networks (social, transportation), route finding algorithms, and representing relationships between entities.

Here's a table summarizing the key differences:

Feature	Tree	Graph
Structure	Hierarchical (single root, no cycles)	Flexible (no root restriction, cycles allowed)
Node connections	One node to zero or more children	Nodes connected by edges (directed/undirected)
Common Implementations	Class with data and children, nested dictionaries	NetworkX library, dictionaries, adjacency lists
Use Cases	Hierarchical data, searching, expressions	Networks, route finding, relationships

In a Nutshell

Abstract data structures are essential tools for organizing and managing data efficiently. Each type has its own strengths and is suited for different scenarios, helping you solve various problems more effectively. Whether you're stacking, queuing, listing, linking, graphing, or branching out, there's a data structure that fits your needs!

Resources

• 🎥 Linked Lists
• 🎥 Stack
• 🎥 Queue
• ADTs